Updates: 10/29/2020 - 1. added explanations for the theorem; 2. added more details to MATLAB figure’s captions; 3. added a nicer formal proof

---

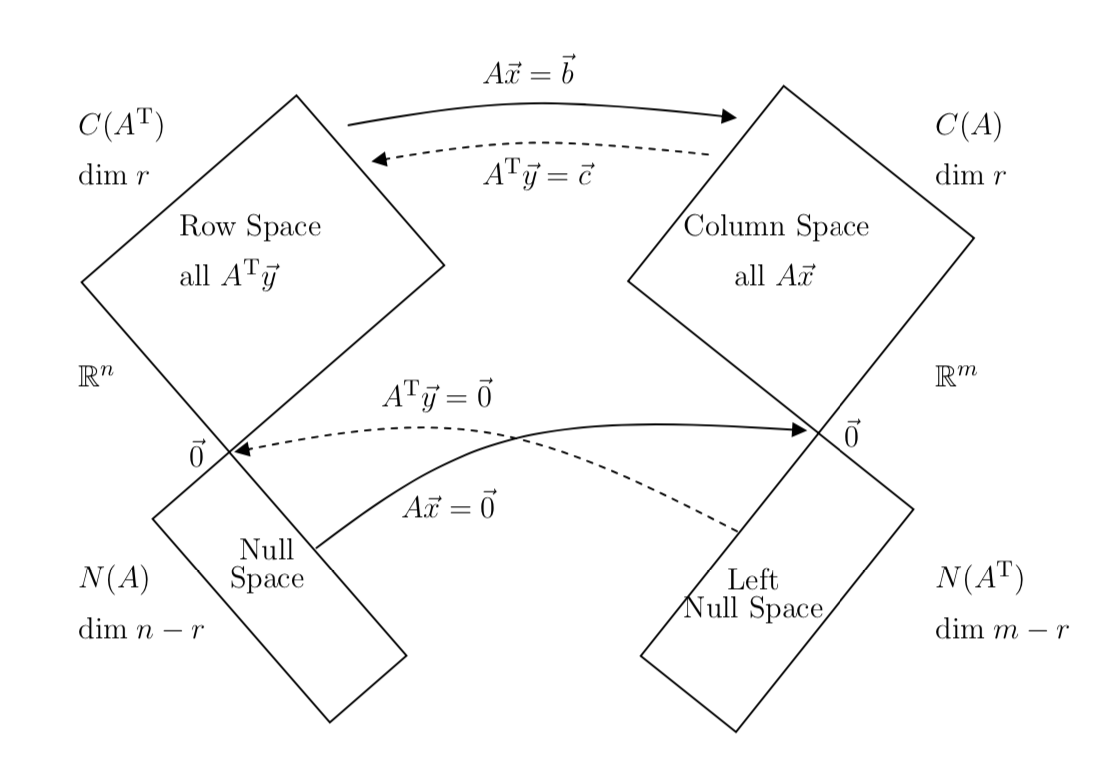
I came across a theorem when struggling with one of the problems from my linear algebra written exam link. Besides from the determinant of block matrix, which I will talk later in another post, the theorem plays an essential role in the linked problem. Here is the theorem below:

Fundamental Theorem of Orthogonality:

Let $A$ be a $m \times n$ matrix. Then,

\[Nul(A^T) = Col(A)^{\perp}\]

In other words, the column space $Col(A)$ contains every vector that is orthogonal to left nullspace $Nul(A^T)$ (in $\mathbb{R}^m$). (Why is column space in $\mathbb{R}^m$? Because every column of $A$ contains $m$ elements.)

Equivalently,

\[\begin{equation*} Nul(A)^{\perp} = Col(A^T) \end{equation*}\]

I.e., the row space $Col(A^T)$ contains every vector that is orthogonal to the nullspace $Nul(A)$ (in $\mathbb{R}^n$). (Again, why are row space and null space in $\mathbb{R}^n$? Because every row of $A$ contains $n$ vectors and so does vecor in null space $x$, where $Ax = 0.$)

Before we see the mathematical proof of the theorem, we shall think about the theorem in an intuitive sense: $Ax = b$ then $b$ is in the column space, which then implies b is perpendicular to the left nullspace.

The above theorem also leads us to the following fundamental theorem:

Rank-Nullity Theorem:

\(\begin{equation*} dim(Col(A)) + dim(Nul(A)) = n \end{equation*}\)

“Strang, G. “Linear Algebra And Its Applications 4th Ed”. Chapter 3.1. New York, Academic Press. 2006.”

Examples:

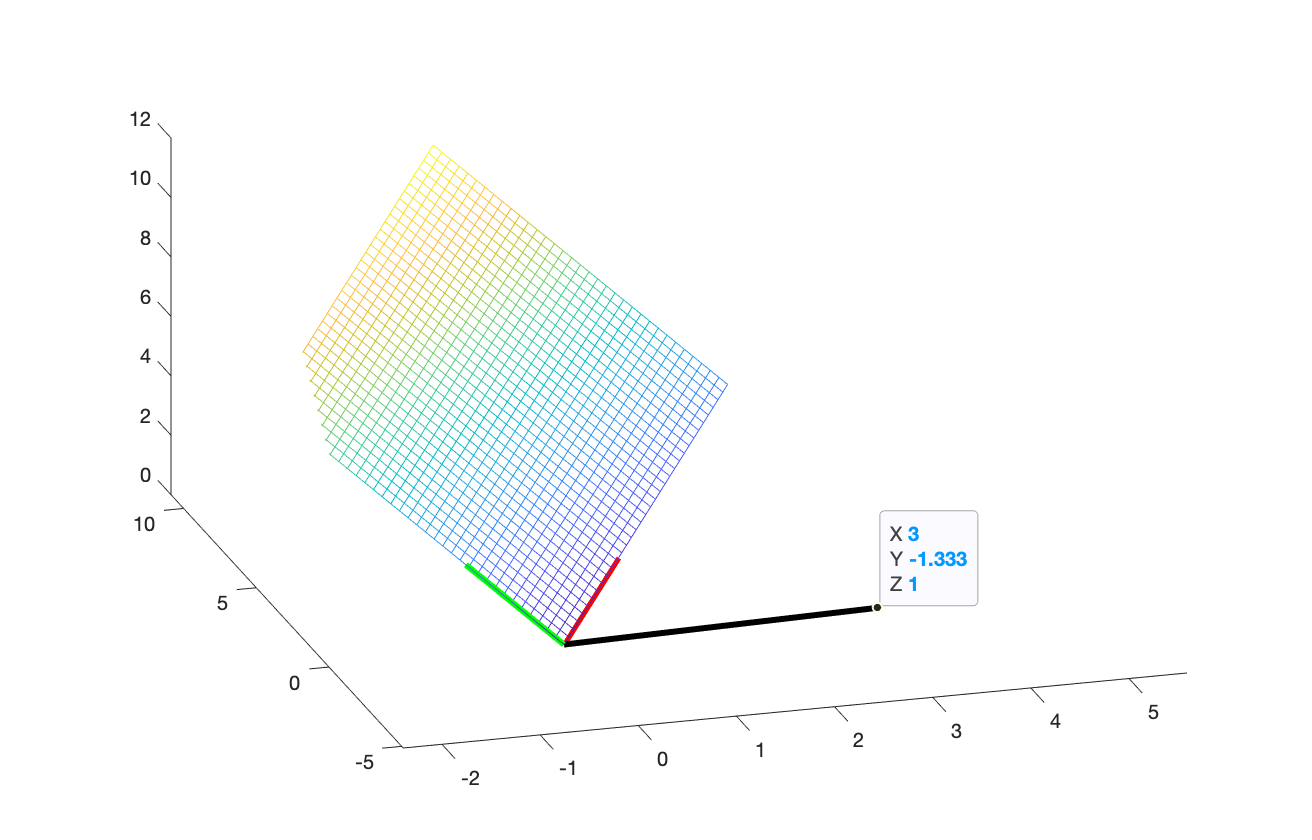
The figures below are generated in MATLAB, notice how the vector (black line) is perpendicular to the plane spanned by two vectors (red and green line):

The orthogonal complement of a 2-d plane spanned by two vectors is a line of a vector in 3-d space.

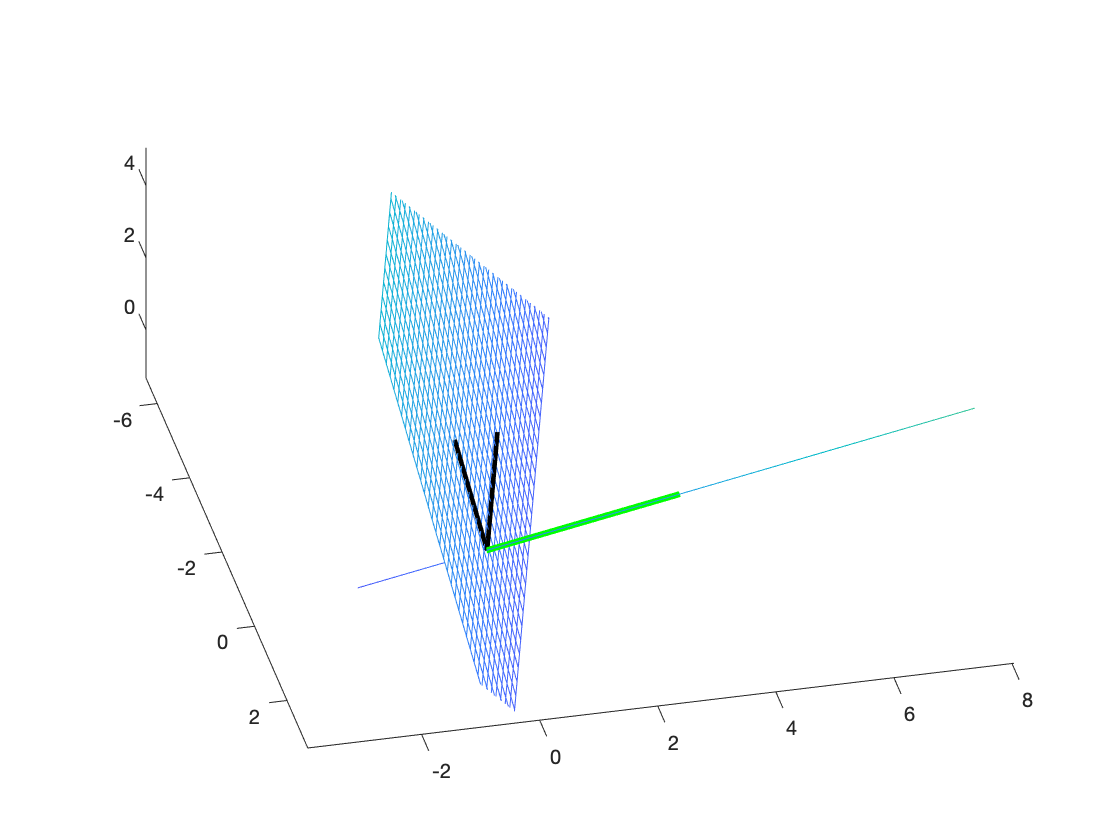
Likewise, the orthogonal complement of a single vector is a 2-d plane in 3-d space.

Now, let us see the proof (it is very straightforward, and you can do on your own and compare):

Proof of the theorem

WTS: $Nul(A^T) = Col(A)^{\perp}$:

$(\subseteq)$ let $x\in Col(A)$, then $x = a_1v_1+a_2v_2+…+a_nv_n, $ where $a_1, a_2, …, a_n$ are columns of $A$, and $v_1, v_2,…, v_n$ are the entries of some vector $v$. 

WTS: $x\perp w$,  where $w\in Nul(A^T)$.

\[\begin{align*} x\cdot w &= x^T w \\ &= (a_1v_1+...+a_nv_n)^T w\\ &=(a_1v_1)^T w+...+(a_nv_n)^T w \\ &= v_1(a_1^Tw) +...+v_n(a_n^Tw)\\ &= v_1(0)+...+v_n(0)\\ &= 0 \\ \end{align*}\] \[\begin{align*} \implies & x \perp w, \forall w \in Nul(A^T) \\ \implies & x\in Nul(A^T)^{\perp} \end{align*}\]

$(\supseteq)$ let $w\in Nul(A^T)$. Then

\[\begin{equation*} a_j^Tw = a_j\cdot w = 0, \forall j = 1,2,...,n \end{equation*}\]

By the definition of orthogonal complement, $w \in Col(A)^{\perp}$. $\Box$

---

WTS: $Nul(A)^{\perp} = Col(A^T)$ or $Nul(A) \perp Col(A^T)$:

Let $x$ be a vector in nullspace where $Ax = 0$. Let $v$ be a vector in row space. Then,

\[v = A^T y, \quad \textrm{for some vector $y$ in column space}\]

And then, we would have

\[v^Tx = (A^Ty)^Tx = y^TAx = y^T0 = 0\]

Thus, $v^T \in Nul(A)$. Therefore, $Nul(A) \perp Col(A^T)$. $\Box$

References

Margalit, D., Rabinoff, J. “Interactive Linear Algebra”. Web. Chapter 6.2. https://textbooks.math.gatech.edu/ila/orthogonal-complements.html

Strang, G. “Linear Algebra And Its Applications 4th Ed”. New York, Academic Press. 2006.